• Texas Hold Em Poker Odds

Texas Hold'em Cheat SheetOdds Based on Outs after the Flop If after the flop, you have: Two outs: Your odds are 11 to 1 (about 8.5 percent) A common scenario would be when you have a pair and you are hoping your pair becomes a three-of-a-kind (a set).

If you are going to ever play at the peak of your game as a poker player, then you have to have a mastery of Texas Hold Em poker odds that is unmatched at the table.

Many players know all about the psychological side of the game and these players are quite good at reading their opponents. Though they can make moves and put their opponents on a hand, poker education is not complete unless you understand some of the math behind the game.

That is where pot odds, implied odds, and the rest of these theories come in handy.

So what is all this about?

What must you learn in order to be successful?

What Are Pot Odds in Poker?

When we talk about Texas Hold Em Poker Odds, we are primarily talking about pot odds.

This is a somewhat imperfect science that gives us a good idea about whether or not a call is in order.

If you are going to make a call, you will want to know that this play is going to give you a chance to win over the long haul.

For that reason, pot odds in poker are highly tied to the idea of variance.

Pot Odds In Holdem

If you are in a pot and you have reasonably put your opponent on a hand, then you can figure out that you have a certain number of outs in the deck.

The odds of winning that hand are one part of the equation, with the other being how much money is in the pot.

If you come to find out that you have a 33% chance of making your hand and taking down the pot, then you should look at the pot to see if you are getting 2:1 or better on your money.

If the pot is $300 and the amount to call is $75, then you would be well advised to make the call. This is due to the fact that you are being offered 4:1 (300/75) on your $75 with a chance of 2:1 to win $300.

In this scenario, you might know that your opponent has you beat at the moment, but the chances of winning the hand, coupled with the relatively small price for seeing an additional card will make this a solid move over the long run.

Why Do These Pot Odds in Poker Matter?

Texas Hold Em Poker odds matter because of the fact that poker is a game of expected value.

If you play enough hands, the amount of money you make is going to correlate closely with the expected value of each of your plays.

For instance, if you are constantly getting your money into the pot with a 56% chance to win, then you will come out ahead in the long run.

Likewise, you need to understand which hands are worth drawing at. Since so much of poker has to do with playing these drawing hands, it is in your best interest to know which hands are going to give you a positive return.

However if you only had a 20% chance to win a hand and you had to pay $100 to win a $200 pot, then making the call would be the wrong move.

In this scenario you would be being offered 2:1 odds ($200/$100) or 33% on your money for a 4:1 or 20% chance to win $200.

You might call and win this time but 80% of the time you will lose!

When you can calculate your poker pot odds on every hand you play, you will have this information at your disposal which your opponent may not. In poker, information is key because it enables you to make quality decisions and increase your expected value over the long run of the play.

How Do You Calculate The Odds Of Making A Poker Hand?

Now that you understand how to calculate pot odds which is crucial for determining whether to call or fold, you are probably wondering just how to come up with the percentages that tell you your chances of winning a specific poker hand.

After all, there is not going to be an ESPN broadcast to put up the win percentage beside your hand like you see on TV!

Lets take a look at how to calculate the odds for making a flush if you need to call to see the next card.

If you are looking to make a specific poker hand you will have a number of outs or remaining cards in the deck that can complete your hand.

In the case that you wish to make a flush, with 2 hearts in your hand and 2 more on the board, you know that there are 9 other hearts in the deck. This is calculated by subtracting the 4 hearts in play from the total 13 hearts in a standard poker deck of 52 cards.

By subtracting the five cards you have seen, your two hole cards and the three cards on the board that make up the flop, from the total 52 cards in the deck gives you 47 remaining cards.

With only 9 cards out of these remaining 47 completing your flush, gives you a rough percentage of around 20% (9/47). That means that the chances of hitting your flush are somewhere in the neighborhood of 20% on the turn.

This means that you would need to be getting 4:1 on your money to make this an acceptable call over the long run.

If intend to call to the river, the chance of hitting your flush with two cards to come increases slightly to 35% or roughly 2:1.

The important thing to remember is that these pot odds calculations are going to be somewhat rough. Without knowing your opponent’s hand or exact information on the available cards in the deck, you are just making an educated guess.

Poker is a game that requires you to make some guesses, though, and the more educated guesses they are, the better your chances of winning the money.

Understanding Implied Odds in Poker

Another concept to consider when thinking about Texas Hold Em Poker odds is the idea of implied odds.

Texas Holdem Pot Odds

This requires you to take into account the amount of money that you might win if you were to hit your hand.

With this principle, if you had something like low connecting cards (56 off suit) and you were sure your opponent had a set, then you might be able to make more money if you hit your straight.

In this case, the opponent probably wouldn’t put you on a straight and wouldn’t be able to lay down his hand. This increases the value of your play by a great deal.

The basic tenet of this philosophy is that if you will win a big pot by hitting a hand, you should be able to call an amount greater than what Texas Hold Em Poker Odds indicates is a correct call. You expect your total winnings to be greater than what is already in the pot.

The concept of implied odds is especially important in No Limit Texas Hold Em since your opponent’s entire stack will be at stake if you hit your draw providing huge implied odds and a big incentive to call.

But remember, you have to be pretty sure that you can win it all for implied odds to work in your favor. This is why it is so important to know your opponent’s style of play and how your opponent perceives you.

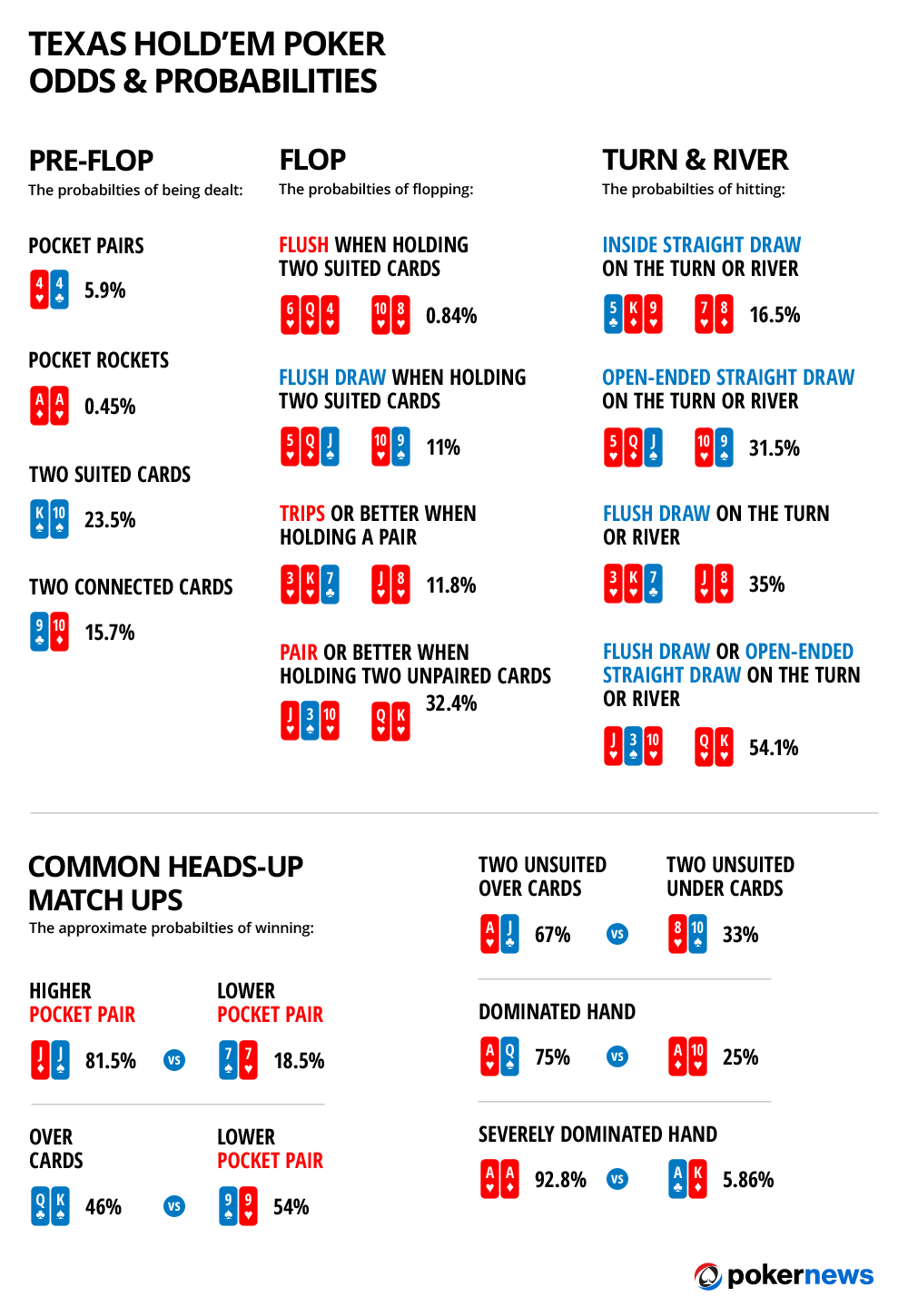
Now that you have a basic understanding of Texas Hold Em Poker odds, how they are calculated, and why they are important, you are ready to take a look at our Texas Hold Em Poker Odds Chart that provides a quick reference guide to the most common and important odds that you need to know while playing the game.

In poker, pot odds are the ratio of the current size of the pot to the cost of a contemplated call.^[1] Pot odds are often compared to the probability of winning a hand with a future card in order to estimate the call's expected value.

• 3Implied pot odds
• 4Reverse implied pot odds
• 5Manipulating pot odds

Texas Holdem Poker Odds Chart

Converting odds ratios to and from percentages[edit]

Odds are most commonly expressed as ratios, but converting them to percentages often make them easier to work with. The ratio has two numbers: the size of the pot and the cost of the call. To convert this ratio to the equivalent percentage, these two numbers are added together and the cost of the call is divided by this sum. For example, the pot is $30, and the cost of the call is $10. The pot odds in this situation are 30:10, or 3:1 when simplified. To get the percentage, 30 and 10 are added to get a sum of 40 and then 10 is divided by 40, giving 0.25, or 25%.

To convert any percentage or fraction to the equivalent odds, the numerator is subtracted from the denominator and then this difference is divided by the numerator. For example, to convert 25%, or 1/4, 1 is subtracted from 4 to get 3 (or 25 from 100 to get 75) and then 3 is divided by 1 (or 75 by 25), giving 3, or 3:1.

Using pot odds to determine expected value[edit]

When a player holds a drawing hand (a hand that is behind now but is likely to win if a certain card is drawn) pot odds are used to determine the expected value of that hand when the player is faced with a bet.

The expected value of a call is determined by comparing the pot odds to the odds of drawing a card that wins the pot. When the odds of drawing a card that wins the pot are numerically higher than the pot odds, the call has a positive expectation; on average, a portion of the pot that is greater than the cost of the call is won. Conversely, if the odds of drawing a winning card are numerically lower than the pot odds, the call has a negative expectation, and the expectation is to win less money on average than it costs to call the bet.

Implied pot odds[edit]

Implied pot odds, or simply implied odds, are calculated the same way as pot odds, but take into consideration estimated future betting. Implied odds are calculated in situations where the player expects to fold in the following round if the draw is missed, thereby losing no additional bets, but expects to gain additional bets when the draw is made. Since the player expects to always gain additional bets in later rounds when the draw is made, and never lose any additional bets when the draw is missed, the extra bets that the player expects to gain, excluding his own, can fairly be added to the current size of the pot. This adjusted pot value is known as the implied pot.

Example (Texas hold'em)[edit]

On the turn, Alice's hand is certainly behind, and she faces a $1 call to win a $10 pot against a single opponent. There are four cards remaining in the deck that make her hand a certain winner. Her probability of drawing one of those cards is therefore 4/47 (8.5%), which when converted to odds is 10.75:1. Since the pot lays 10:1 (9.1%), Alice will on average lose money by calling if there is no future betting. However, Alice expects her opponent to call her additional $1 bet on the final betting round if she makes her draw. Alice will fold if she misses her draw and thus lose no additional bets. Alice's implied pot is therefore $11 ($10 plus the expected $1 call to her additional $1 bet), so her implied pot odds are 11:1 (8.3%). Her call now has a positive expectation.

Reverse implied pot odds[edit]

Reverse implied pot odds, or simply reverse implied odds, apply to situations where a player will win the minimum if holding the best hand but lose the maximum if not having the best hand. Aggressive actions (bets and raises) are subject to reverse implied odds, because they win the minimum if they win immediately (the current pot), but may lose the maximum if called (the current pot plus the called bet or raise). These situations may also occur when a player has a made hand with little chance of improving what is believed to be currently the best hand, but an opponent continues to bet. An opponent with a weak hand will be likely to give up after the player calls and not call any bets the player makes. An opponent with a superior hand, will, on the other hand, continue, (extracting additional bets or calls from the player).

Limit Texas hold'em example[edit]

With one card to come, Alice holds a made hand with little chance of improving and faces a $10 call to win a $30 pot. If her opponent has a weak hand or is bluffing, Alice expects no further bets or calls from her opponent. If her opponent has a superior hand, Alice expects the opponent to bet another $10 on the end. Therefore, if Alice wins, she only expects to win the $30 currently in the pot, but if she loses, she expects to lose $20 ($10 call on the turn plus $10 call on the river). Because she is risking $20 to win $30, Alice's reverse implied pot odds are 1.5-to-1 ($30/$20) or 40 percent (1/(1.5+1)). For calling to have a positive expectation, Alice must believe the probability of her opponent having a weak hand is over 40 percent.

Manipulating pot odds[edit]

Often a player will bet to manipulate the pot odds offered to other players. A common example of manipulating pot odds is make a bet to protect a made hand that discourages opponents from chasing a drawing hand.

No-limit Texas hold 'em example[edit]

With one card to come, Bob has a made hand, but the board shows a potential flush draw. Bob wants to bet enough to make it wrong for an opponent with a flush draw to call, but Bob does not want to bet more than he has to in the event the opponent already has him beat.

Assuming a $20 pot and one opponent, if Bob bets $10 (half the pot), when his opponent acts, the pot will be $30 and it will cost $10 to call. The opponent's pot odds will be 3-to-1, or 25 percent. If the opponent is on a flush draw (9/46, approximately 19.565 percent or 4.11-to-1 odds against with one card to come), the pot is not offering adequate pot odds for the opponent to call unless the opponent thinks they can induce additional final round betting from Bob if the opponent completes their flush draw (see implied pot odds).

A bet of $6.43, resulting in pot odds of 4.11-to-1, would make his opponent mathematically indifferent to calling if implied odds are disregarded.

Bluffing frequency[edit]

According to David Sklansky, game theory shows that a player should bluff a percentage of the time equal to his opponent's pot odds to call the bluff. For example, in the final betting round, if the pot is $30 and a player is contemplating a $30 bet (which will give his opponent 2-to-1 pot odds for the call), the player should bluff half as often as he would bet for value (one out of three times).

However, this conclusion does not take into account some of the context of specific situations. A player's bluffing frequency often accounts for many different factors, particularly the tightness or looseness of their opponents. Bluffing against a tight player is more likely to induce a fold than bluffing against a loose player, who is more likely to call the bluff. Sklansky's strategy is an equilibrium strategy in the sense that it is optimal against someone playing an optimal strategy against it.

See also[edit]

Notes[edit]

References[edit]

• David Sklansky (1987). The Theory of Poker. Two Plus Two Publications. ISBN1-880685-00-0.
• David Sklansky (2001). Tournament Poker for Advanced Players. Two Plus Two Publications. ISBN1-880685-28-0.
• David Sklansky and Mason Malmuth (1988). Hold 'em Poker for Advanced Players. Two Plus Two Publications. ISBN1-880685-22-1.
• Dan Harrington and Bill Robertie (2004). Harrington on Hold'em: Expert Strategy For No-Limit Tournaments; Volume I: Strategic Play. Two Plus Two Publications. ISBN1-880685-33-7.
• Dan Harrington and Bill Robertie (2005). Harrington on Hold'em: Expert Strategy For No-Limit Tournaments; Volume II: The Endgame. Two Plus Two Publications. ISBN1-880685-35-3.
• David Sklansky and Ed Miller (2006). No Limit Hold 'Em Theory and Practice. Two Plus Two Publications. ISBN1-880685-37-X.